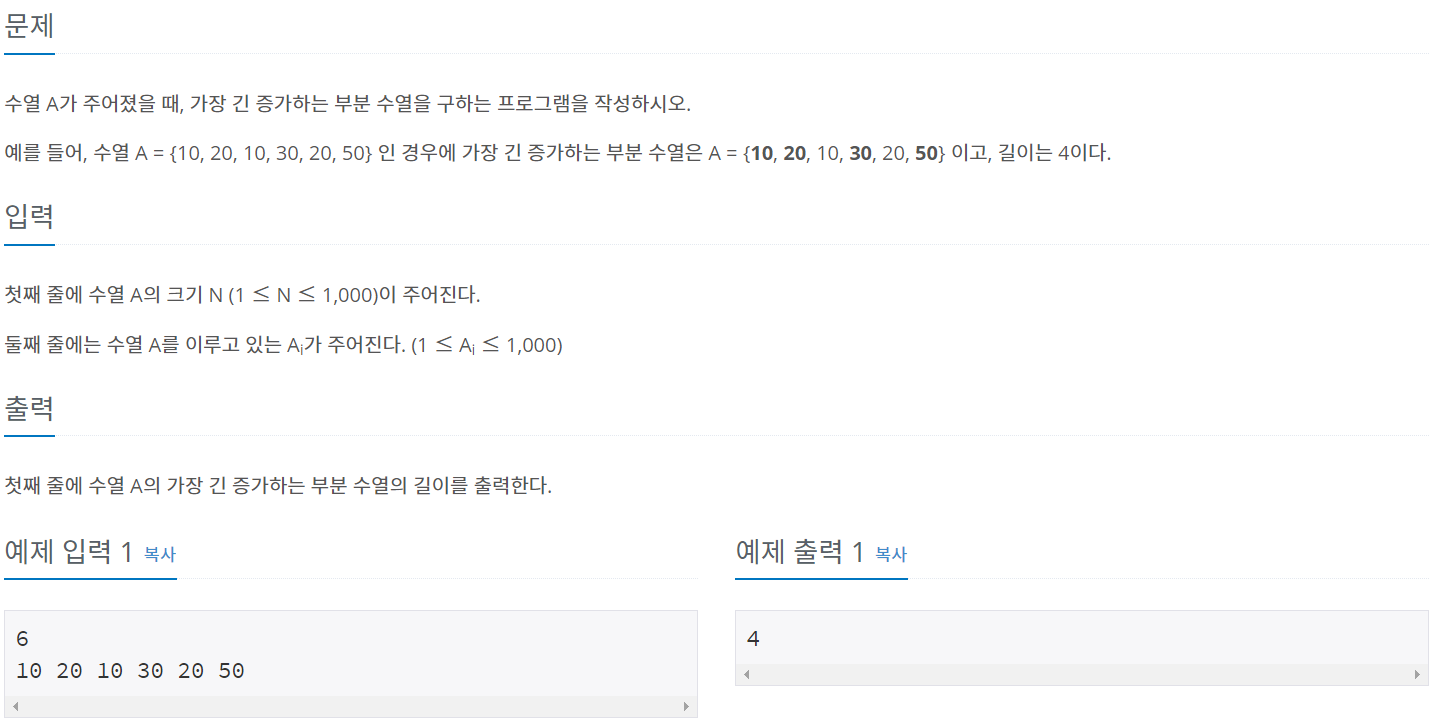
풀이
위의 문제는 대표적인 LIS문제로 dp를 이용해 푸는 문제이다. 만약 LIS알고리즘을 돌렸을때 특정 인덱스에서 현재의 값(seq)이 이전 인덱스의 값(seq)보다 크다면 이전 인덱스에서 만족하는 부분수열은 자연스럽게 만족하므로 현재위치의 dp는 특정인덱스의 dp에 +1을 하면 된다. (이전 인덱스의 수 또한 포함하므로.) 유사한 문제로 포도주문제나 계단오르기 가 있다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int N;
static Integer[] seq;
static Integer[] dp;
public static void main(String[] args)throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), "");
N = Integer.parseInt(st.nextToken());
seq = new Integer[N];
dp = new Integer[N];
st = new StringTokenizer(br.readLine(), " ");
for(int i=0; i<N; i++){
seq[i] = Integer.parseInt(st.nextToken());
}
for(int i=0; i<N; i++){
LIS(i);
}
int max = dp[0];
for(int i=0; i<N; i++){
max = Math.max(max, dp[i]);
}
System.out.println(max);
}
public static int LIS(int x){
if(dp[x]==null){
dp[x] = 1;
for(int i=x-1; i>=0; i--){
if(seq[x] > seq[i]){
dp[x] = Math.max(dp[x], LIS(i)+1);
}
}
}
return dp[x];
}
}'백준' 카테고리의 다른 글
| [백준] 11729 하노이 탑 이동 순서 (JAVA) (0) | 2021.08.21 |
|---|---|
| [백준] 1931 회의실 배정 (JAVA) (0) | 2021.08.21 |
| [백준] 1012 유기농배추(JAVA) (0) | 2021.08.20 |
| [백준] 1260 DFS와BFS (JAVA) (0) | 2021.08.18 |
| [백준 ]11401 이항계수 3 (JAVA) (0) | 2021.08.15 |


