
https://www.acmicpc.net/problem/1932
1932번: 정수 삼각형
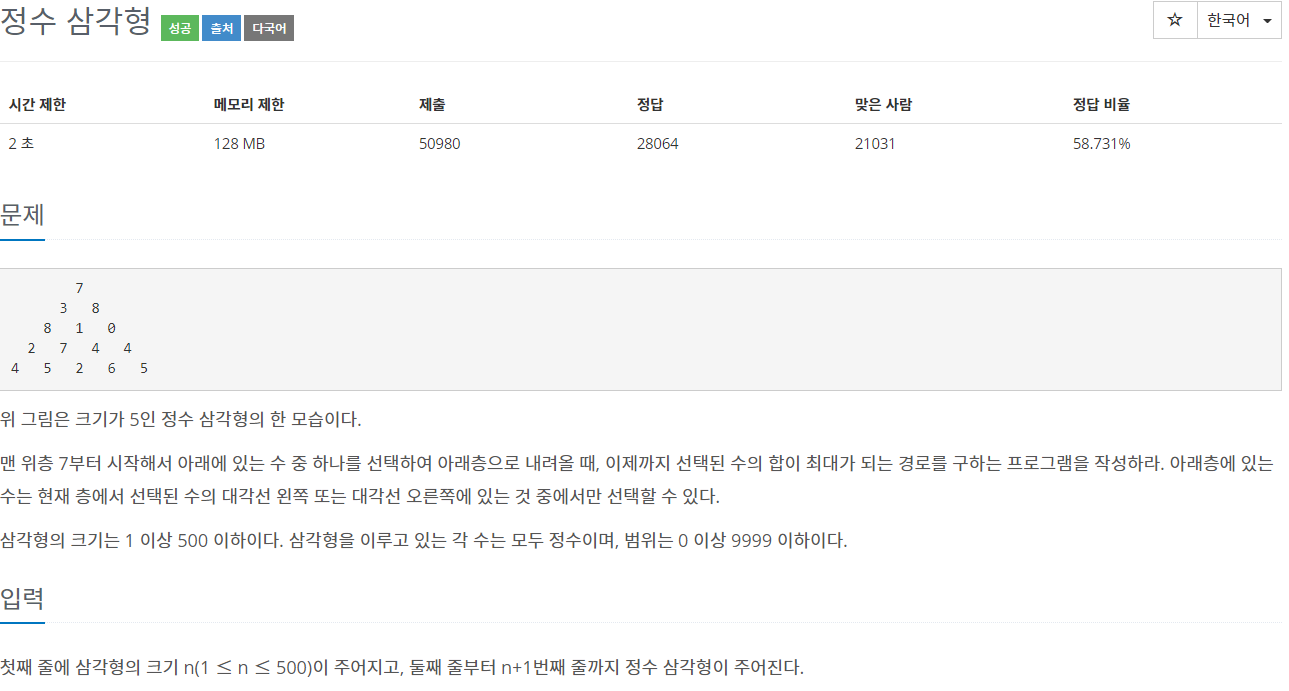
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
www.acmicpc.net
풀이
이 문제는 전형적인 DP로 DP를 조금 풀어보았더라면 쉽게 해결할수있는 문제이다. 알고리즘의 개요는 이러하다. 위에서부터 내려오는 방식과 밑에서부터 올라가는 방식이 있는데 나는 밑에서부터 올라가는 방식을 사용해서 문제를 해결했다. 우선 DP라는 2차원 배열과 ary이라는 2차원배열을 생성후 입력값을 ary에 저장한다. 그러고 난뒤 가장 ary의 가장 아랫부분을 dp에 저장하고 그 다음에는 다음과 같은 식을 수행한다
dp[i][j] = ary[i][j] + Math.max(dp[i+1][j], dp[i+1][j+1])
위의 코드를 수행하면 dp[i][j]에는 가장 최대의 값이 저장되고 그렇게 하다보면 마지막에는 dp[0][0]에는 최대값이 저장된다. 그러므로 dp[0][0]을 출력하면 정답이 된다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class Main{
public static int[][] ary;
public static int[][] dp;
public static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
n = Integer.parseInt(br.readLine());
ary = new int[n][n];
dp = new int[n][n];
for(int i=0; i<n; i++){
st = new StringTokenizer(br.readLine(), " ");
for(int j=0; j<=i; j++){
ary[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int i=0; i<n; i++){
dp[n-1][i] = ary[n-1][i];
}
for(int i=n-2; i>=0; i--){
for(int j=0; j<=i; j++){
dp[i][j] = ary[i][j] + Math.max(dp[i+1][j], dp[i+1][j+1]);
}
}
System.out.println(dp[0][0]);
}
}'백준' 카테고리의 다른 글
| [백준] 2156 포도주 시식 (JAVA) (0) | 2021.09.21 |
|---|---|
| [백준] 2579 계단 오르기 (JAVA) (0) | 2021.09.21 |
| [백준] 1697 숨바꼭질 (JAVA) (0) | 2021.09.20 |
| [백준] 7576 토마토 (JAVA) (0) | 2021.09.15 |
| [백준] 1149 RGB거리 (JAVA) (0) | 2021.09.15 |



